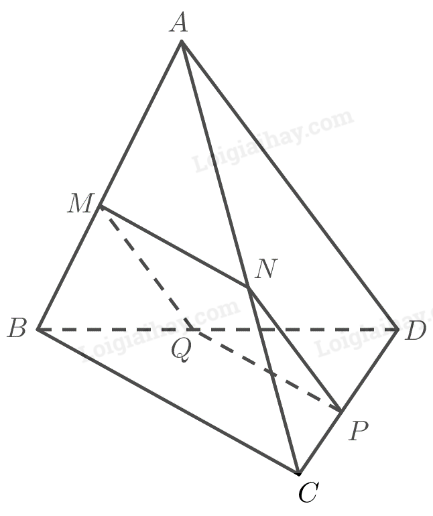
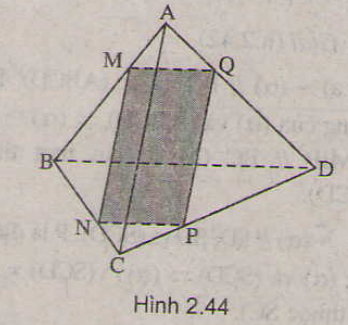
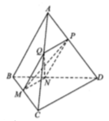
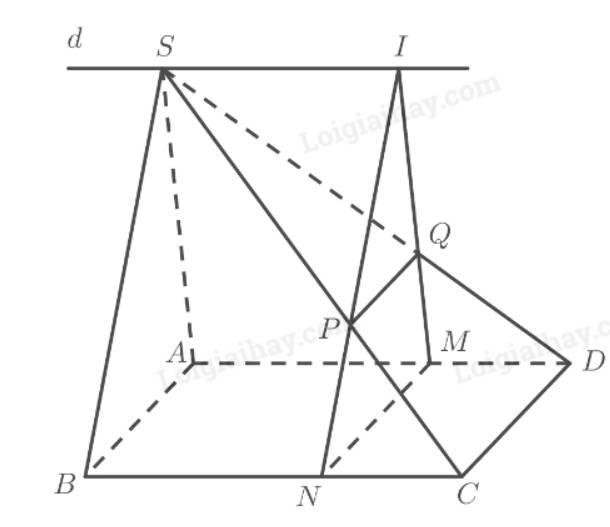
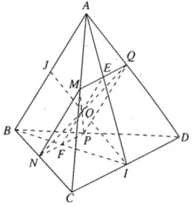
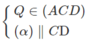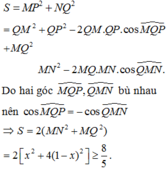Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng \(\left(\alpha\right)\) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P, Q
a) Tứ giác MNPQ là hình gì ?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC ?





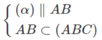
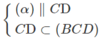
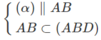 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB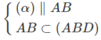 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD